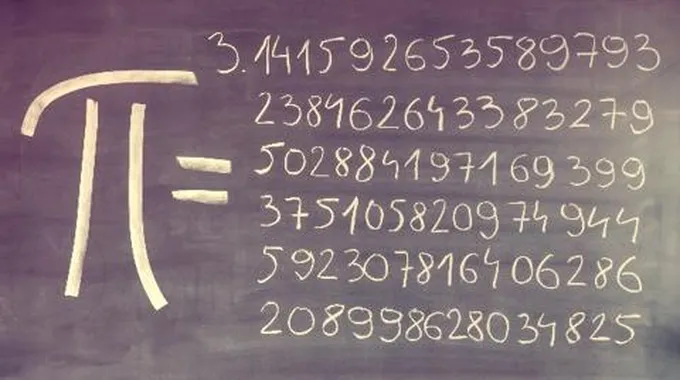أحد الثوابت الأكثر استخدامًا في الرياضيات هو الرقم باي pi، والذي يُشار إليه بالحرف اليوناني π. نشأ مفهوم pi في الهندسة، ولكن هذا الرقم له تطبيقات في جميع أنحاء الرياضيات ويظهر في مواضيع متعددة بما في ذلك الإحصاء والاحتمالات.
قيمة الرقم باي Pi.
يتم تعريف الرقم باي Pi على أنه نسبة محيط الدائرة إلى قطرها. قيمة pi أكبر قليلاً من ثلاثة، مما يعني أن كل دائرة في الكون لها محيط يزيد طولها قليلاً عن ثلاثة أضعاف قطرها.
بتعبير أدق، يحتوي pi على تمثيل عشري يبدأ 3.14159265 … هذا جزء فقط من التوسع العشري لـ pi.
أول 100 خانة من الرقم باي:
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067
معلومات عن الرقم باي Pi.
يحتوي Pi على العديد من الميزات الرائعة وغير العادية، بما في ذلك:
- الرقم باي Pi هو رقم حقيقي غير منطقي. هذا يعني أنه لا يمكن التعبير عن pi ككسر a / b حيث a و b كلاهما عدد صحيح. على الرغم من أن الأرقام 22/7 و 355/113 مفيدة في تقدير pi، إلا أن أيا من هذه الكسور لا يمثل القيمة الحقيقية لـ pi.
- نظرًا لأن pi رقم غير نسبي، فإن توسعه العشري لا ينتهي أبدًا أو يتكرر. هناك بعض الأسئلة المتعلقة بهذا التوسع العشري، مثل: هل تظهر كل سلسلة ممكنة من الأرقام في مكان ما في التوسع العشري لـ pi؟ إذا ظهرت كل سلسلة ممكنة، فسيكون رقم هاتفك الخلوي في مكان ما في توسيع pi (ولكن هذا هو الحال بالنسبة لأي شخص آخر).
- الرقم باي Pi هو رقم متسامي. هذا يعني أن pi ليس صفرًا لكثير الحدود مع معامِلات عدد صحيح. هذه الحقيقة مهمة عند استكشاف المزيد من الميزات المتقدمة لـ pi.
- الرقم باي Pi مهم هندسيًا، وليس فقط لأنه يربط محيط الدائرة وقطرها. يظهر هذا الرقم أيضًا في معادلة مساحة الدائرة. مساحة دائرة نصف قطرها r هي A = pi r2. يتم استخدام الرقم pi في الصيغ الهندسية الأخرى، مثل مساحة السطح وحجم الكرة وحجم المخروط وحجم الأسطوانة ذات القاعدة الدائرية.
- يظهر Pi عندما لا يكون متوقعًا. للحصول على أحد الأمثلة العديدة لذلك، ضع في اعتبارك المجموع اللامتناهي 1 + 1/4 + 1/9 + 1/16 + 1/25 + … يتقارب هذا المجموع مع القيمة pi 2 / 6.
إقرأ أيضاً… حيل وخدع مذهلة في الرياضيات.
الرقم باي Pi في الإحصاء والاحتمالات.
يُظهر Pi مظاهرًا مدهشة في الرياضيات، وبعض هذه المظاهر في مواضيع الاحتمالات والإحصاء. تتميز معادلة التوزيع الطبيعي القياسي، والمعروفة أيضًا باسم منحنى الجرس، بالرقم pi باعتباره ثابتًا للتطبيع.
بعبارة أخرى، تتيح لك القسمة على تعبير يتضمن pi القول إن المساحة الواقعة أسفل المنحنى تساوي واحدًا. الرقم Pi هو جزء من معادلات التوزيعات الاحتمالية الأخرى أيضًا.
حدث مفاجئ آخر للرقم باي في الاحتمال هو تجربة رمي الإبر التي استمرت قرونًا. في القرن الثامن عشر، طرح جورج لويس لوكلير، كونت دي بوفون سؤالاً يتعلق باحتمالية سقوط الإبر: ابدأ بأرضية بألواح خشبية بعرض موحد تكون فيها الخطوط بين كل لوح متوازي مع بعضها البعض.
خذ إبرة بطول أقصر من المسافة بين الألواح. إذا أسقطت إبرة على الأرض، فما احتمال سقوطها على خط بين لوحين من الخشب؟ كما اتضح، فإن احتمال أن تهبط الإبرة على خط بين لوحين هو ضعف طول الإبرة مقسومًا على الطول بين اللوحين مضروبًا في pi.