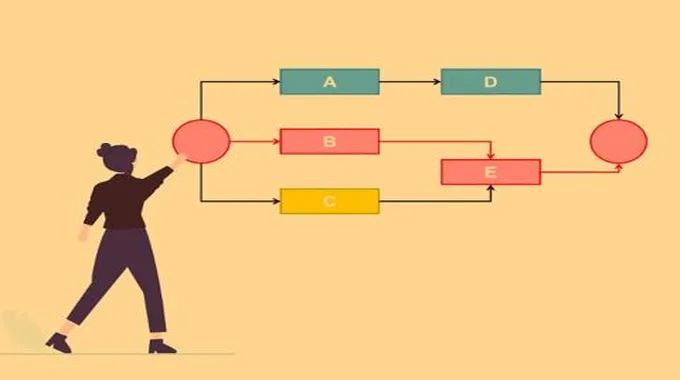
تحليل المسار في الاحصاء هو شكل من أشكال التحليل الإحصائي للانحدار المتعدد الذي يستخدم لتقييم النماذج السببية من خلال فحص العلاقات بين متغير تابع ومتغيرين مستقلين أو أكثر.
باستخدام هذه الطريقة، يمكن للمرء تقدير حجم وأهمية الروابط السببية بين المتغيرات.
تحليل المسار.
من خلال إجراءئه، يمكن للباحثين فهم العلاقات السببية بين المتغيرات المختلفة بشكل أفضل. للبدء، يرسم الباحثون مخططًا يعمل بمثابة تمثيل مرئي للعلاقة بين المتغيرات.
بعد ذلك، يستخدم الباحثون برنامجًا إحصائيًا (مثل SPSS أو STATA) لمقارنة توقعاتهم بالعلاقة الفعلية بين المتغيرات.
أهمية تحليل المسار.
يعد تحليل المسار مفيدًا من الناحية النظرية لأنه، على عكس التقنيات الأخرى، يجبرنا على تحديد العلاقات بين جميع المتغيرات المستقلة. ينتج عن هذا نموذج يظهر الآليات السببية التي من خلالها تنتج المتغيرات المستقلة تأثيرات مباشرة وغير مباشرة على متغير تابع.
تم تطويره بواسطة عالم الوراثة Sewall Wright في عام 1918. وبمرور الوقت تم تبني الطريقة في العلوم الفيزيائية والعلوم الاجتماعية الأخرى، بما في ذلك علم الاجتماع.
يمكن للمرء اليوم إجراؤه مع البرامج الإحصائية بما في ذلك SPSS و STATA، من بين أمور أخرى. تُعرف الطريقة أيضًا باسم النمذجة السببية، وتحليل هياكل التغاير، والنماذج المتغيرة الكامنة.
المتطلبات الأساسية لإجراء تحليل المسار.
هناك نوعان من المتطلبات الرئيسية من أجل إجراء التحليل:
- يجب أن تسير جميع العلاقات السببية بين المتغيرات في اتجاه واحد فقط (لا يمكن أن يكون لديك زوج من المتغيرات التي تسبب بعضها البعض)
- يجب أن يكون للمتغيرات ترتيب زمني واضح حيث لا يمكن القول أن أحد المتغيرات يتسبب في متغير آخر ما لم يسبقه في الوقت المناسب.
إقرأ أيضاً… ما هو الوسيط في الرياضيات والإحصاء؟ وكيف يمكن حسابه؟
كيفية استخدام تحليل المسار.
عادةً ما يتضمن إنشاء مخطط مسار يتم فيه تحديد العلاقات بين جميع المتغيرات والاتجاه السببي بينها على وجه التحديد.
عند إجراء تحليل المسار، يمكن للمرء أولاً إنشاء مخطط مسار الإدخال، والذي يوضح العلاقات المفترضة. في مخطط المسار، يستخدم الباحثون الأسهم لإظهار كيفية ارتباط المتغيرات المختلفة ببعضها البعض.
يظهر سهم يشير من المتغير (أ) إلى المتغير (ب)، على سبيل المثال، أن المتغير (أ) يُفترض أنه يؤثر على المتغير (ب).
بعد الانتهاء من التحليل الإحصائي، يقوم الباحث بعد ذلك بإنشاء مخطط مسار الإخراج، والذي يوضح العلاقات كما هي موجودة بالفعل بحسب التحليل الذي تم إجراؤه.
إذا كانت فرضية الباحث صحيحة، فسيعرض مخطط مسار الإدخال ومخطط مسار الإخراج نفس العلاقات بين المتغيرات.
أمثلة على تحليل المسار في البحث.
لنفكر في مثال قد يكون فيه هذا التحليل مفيدًا. لنفترض أنك تفترض أن للعمر تأثيرًا مباشرًا على الرضا الوظيفي، وتفترض أن له تأثيرًا إيجابيًا، بحيث يكون العمر أكثر رضىًا عن وظيفته.
سيدرك الباحث الجيد أن هناك بالتأكيد متغيرات مستقلة أخرى تؤثر أيضًا على متغيرنا التابع للرضا الوظيفي: على سبيل المثال، الاستقلالية والدخل، من بين أمور أخرى.
باستخدام تحليل المسار، يمكن للباحث إنشاء رسم تخطيطي يرسم العلاقات بين المتغيرات. سيُظهر الرسم البياني ارتباطًا بين العمر والاستقلالية (لأنه عادةً ما يكون الأقدم هو الدرجة الأكبر من الاستقلالية التي يتمتعون بها)، وبين العمر والدخل (مرة أخرى، تميل العلاقة الإيجابية بين الاثنين).
بعد ذلك، يجب أن يُظهر الرسم البياني أيضًا العلاقات بين هاتين المجموعتين من المتغيرات والمتغير التابع: الرضا الوظيفي.
بعد استخدام برنامج إحصائي لتقييم هذه العلاقات، يمكن عندئذٍ إعادة رسم الرسم التخطيطي للإشارة إلى حجم العلاقات وأهميتها.
على سبيل المثال، قد يجد الباحث أن كلا من الاستقلالية والدخل مرتبطان بالرضا الوظيفي، وأن أحد هذين المتغيرين له صلة أقوى بكثير بالرضا الوظيفي من الآخر، أو أن أيًا من المتغيرين له صلة كبيرة بالرضا الوظيفي.
إقرأ أيضاً… طرق تحليل البيانات في اكسل التي يجب معرفتها.
نقاط القوة والضعف في تحليل المسار.
في حين أن تحليل المسار مفيد لتقييم الفرضيات السببية، فإن هذه الطريقة لا يمكنها تحديد اتجاه السببية. يوضح الارتباط ويشير إلى قوة الفرضية السببية، لكنه لا يثبت اتجاه السببية.
من أجل فهم اتجاه السببية تمامًا، يمكن للباحثين التفكير في إجراء دراسات تجريبية يتم فيها تعيين المشاركين بشكل عشوائي لمجموعة العلاج والمراقبة.